This week is focused on the optimization and training process. In particular, this week covers ways to make the training process faster and more efficient, allowing us to iterate more quickly when trying different approaches.
This week’s topics are:
- Mini-batch Gradient Descent
- Exponentially Weighted Moving Averages (EWMA)
- Gradient Descent with Momentum
- RMSProp
- Adam
- Learning Rate Decay
Mini-batch Gradient Descent
We discussed gradient descent briefly on the second week of the first course. A key takeaway is that vanilla gradient descent is vectorized across all our training samples $x^{(m)}$. That is, every gradient step is taken after doing a forward and back propagation over our entire training data. This is relatively efficient when our data is small, but as our data grows it becomes a very big challenge. This is especially true with large neural networks or complex architectures.
The process described above is called batch gradient descent, that is a batch is our entire training set $M_{train}$. The name batch gradient descent is an artifact of history, so just take it as it is. Remember that batch gradient descent is the gradient descent version that uses all of our training samples.
As we might imagine, mini-batch gradient descent is running gradient descent on smaller batches of our data. Formally a mini-batch is a subset of our training samples and labels, $X, Y$. We refer to batch $t$ by the tuple $(X^{\{t\}}, Y^{\{t\}})`. For example if we have $m = 5,000,000$ training samples. We might generate $5,000$ mini-batches of $1,000$ samples each. If the dimensions of $X$ are $(N_x, m)$, then the dimensions of $X^{\{t\}}$ should be $(N_x, 1000)$, and those of $Y^{\{t\}}$ should be $(1, 1000)$.
The whole idea is that instead of using $X, Y$ when running gradient descent, we loop over every batch $X^{\{t\}}, Y^{\{t\}}$. On each iteration we run the vectorized implementation of our network’s forward propagation over each batch, in this case $1,000$ samples. After this, we run the back propagation and update the parameters based on the gradients with respect to the cost function over each batch. One pass over all our batches is called an epoch. So far, this is nothing new, just chunking gradient descent to have finer-grained chunks.
But why does this work? Imagine that we set our batch to be $m_b = 1$, that is, on each iteration we will simply look at one training sample and run gradient descent. If the sample we use on each iteration is random, then this process is called stochastic gradient descent. It turns out that on every iteration, gradient descent will take a step independent of other samples in our data, so the “path down the mountain” of gradient descent will look like a blind-wandering, kinda like Brownian motion. Think of a drunk version of gradient descent. It will also be slower because we loose the optimization that arises from vectorization, but still faster than batch gradient descent. On the other hand, imagine that $m_b = m$ so that we have a single batch, our entire data set. Now we are back to batch gradient descent, and each iteration step of gradient descent is taken by averaging each of the samples’ contribution to the gradient. The “path down the mountain” looks much more purposeful and directed, because we have a larger sample. The tradeoff is in the amount of noise that results from smaller samples sizes as we decrease our batch size. Somewhere in between $m_b = 1$ and $m_b = m$ there is a sweet spot that allows us to iterative fast but without much random meandering.
If our data set is small $m \leq 2000$ then running batch gradient descent should be close to optimal in terms of speed. Otherwise, using mini-batch gradient descent will usually be faster. Batch sizes is really a hyperparameter that we might search for, however, usually it’s some multiple of $2^n$, such as $64, 128, 256, 512$. Usually we select this based on amount of memory on our machine in the case that we cannot fit all our data in memory at once.
An important consideration is that the data should be randomly shuffled before generating the batches. So that they really are random samples of $X, Y$ without replacement.
Exponentially Weighted Moving Averages (EWMA)
EWMA is a central component of other optimization algorithms that build upon gradient descent. If we have ever tried to code up a moving average, we might have noticed that it is very memory inefficient, especially if we want to do it in a vectorized fashion. EWMA is a solution with a memory complexity of $O(1)$ that approximates a moving average over an arbitrary number of periods. We will later see how this is applied within the context of gradient descent. Let’s first look at what exponentially weighted averages are.
Say that we have a sequence of observations over time from the same source; that is a time-series measurement. Let $\theta_t$ be the measurement in period $t$. A very common thing to do with time-series is to smoothen the time-series. A common approach is to use a moving average: at every period $t$ we look behind some number of periods, and calculate the average and assign that to a new time-series $V_t$, and so on. If we use a 7-period moving average, we will lose first 7 periods. There is another way that approximates this, and it’s defined as this:
$$ \begin{equation} V_t = \beta V_{t-1} + (1-\beta)\theta_t \end{equation} $$
That is, each smoothed value $V_t$ is some combination of the previous one $V_{t-1}$ and the current one $\theta_t$ scaled by $\beta$ and $(1-\beta)$, thinking about $\beta$ as the mix between the past and today. The nice thing is that we can go from values of $\beta$ to the number of periods pretty easily: when $\beta = 0.9$ we are approximately averaging over the last 10 periods. If we set $\beta = 0.98$ then this is approximately averaging over the last 50 periods. If we set $\beta = 0.5$ then this is approximately averaging over the last 2 periods. Think about what happens when $\beta=1$.
There is a nice explanation of why this approximates a regular moving average on the course, but I think the details are fine to be left out for now.
In practice, we usually initialize $V_t = 0$ and loop over our periods to calculate all $V_t$ for each period $t$.
Bias Correction
If we initialize $V_t = 0$, then we might imagine that our initial $V_t$s will be heavily biased downwards. The bias will eventually disappear as we move through our time periods. It turns out that there is a way to correct the bias with a simple scaling procedure:
$$ \begin{equation} V_t = \frac{\beta V_{t-1} + (1-\beta)\theta_t}{1 - \beta^t} \end{equation} $$
Notice the term $\beta^t$ in the denominator. When $t$ is small, i.e. our initial periods, then $V_t$ will be scaled upwards. As we move down our time-series, the bias correction will be much smaller since $\beta^t$ will become much smaller since $0 < \beta \leq 1$.
Gradient Descent with Momentum
Let’s come back from the time-series digression. Why did we go over moving averages on time-series? Remember that when we introduced mini-batch gradient descent we mentioned that the “path down the mountain” will be more “noisy”. From the extreme of using a batch of size $1$, which is the most “noisy” up to using our entire data, which is the least noisy. It turns out that we can use the concept of EWMA to give “inertia” to the steps “down the mountain” that mini-batch gradient descent takes. This is called momentum, and it uses EWMA of the gradients to take steps, instead of each gradient being independently evaluated.
Remember that in physics, momentum is a vector: $\mathbf{p} = m\mathbf{v}$ since $\mathbf{v}$ is the velocity vector. While inertia is a scalar!
The idea is exactly the same as when we want to smooth time-series. In this case we want to smooth the oscillations of the cost function as we iterate over each mini-batch. Think that if the oscillations along one dimensions are higher, those will be dampened more than a dimension with fewer oscillations.
Technically, this means that when we update $W^{[l]}$, we not only need to calculate the gradient $dW^{[l]}$, we need to also calculate the EWMA of the gradients:
$$ \begin{equation} v_{dW^{[l]}} = \beta v_{dW^{[l]}} + (1-\beta) dW^{[l]} \end{equation} $$
And the parameter update becomes:
$$ \begin{equation} W^{[l]} = W^{[l]} - \alpha v_{dW^{[l]}} \end{equation} $$
Notice that in practice many people don’t use bias correction, and that the example above is only for the $W^{[l]}$ parameters. This should also be repeated for the $b^{[l]}$ parameters. Finally, the choice of $\beta$ is now part of hyperparameter tuning, but almost everyone uses $\beta = 0.9$, which approximates averaging over the last 10 gradient iterations. In a nutshell, momentum accelerates our search in the direction of the minima (and away from oscillations) using EWMA. Finally, notice that we are updating our parameters directly with the EWMA of the gradients. We will do something slightly different next.
RMSProp
RMSProp (root-mean-square propagation) is a cousin of the momentum idea. However, instead of using the EWMA of the gradients for the update, we scale the gradient with the EWMA of the squares of the gradients. 1 If this is confusing, looking at the equation below might help:
$$ \begin{equation} S_{dW^{[l]}} = \beta S_{dW^{[l]}} + (1-\beta) dW^{[l]2} \end{equation} $$
And the parameter update:
$$ \begin{equation} W^{[l]} = W^{[l]} - \alpha \frac{dW^{[l]}}{\sqrt{S_{dW^{[l]}}}+ \epsilon} \end{equation} $$
Where $\epsilon = 10^{-8}$ is a constant that guarantees numerical stability.
The idea is similar to momentum, only that with the case of RMSProp we are shrinking the gradient by the square root of the squared EWMA of the gradients. This in turn means that the gradient dimension with the largest oscillation will be dampened proportionally to its size. In a nutshell, RMSProp constrains the oscillations away from the minima, also using EWMA. Intuitively, this is what’s happening when we scale down our gradient by the squared EWMA of the gradient.
Adam
Adam is usually introduced as a combination of momentum and RMSProp. It turns out that Adam has been shown to be more flexible and generalizable than momentum. 2
The update step is literally combining momentum and RMSProp, and again we will only go over the $W^{[l]}$ update, ignoring the $b^{[l]}$ update for conciseness. We initialize $V_{dW^{[l]}}, S_{dW^{[l]}} = 0$:
$$ \begin{align} V_{dW^{[l]}} &= \beta_1 V_{dW^{[l]}} + (1-\beta_1)dW^{[l]} \\ S_{dW^{[l]}} &= \beta_2 S_{dW^{[l]}} + (1-\beta_2)dW^{[l]2} \end{align} $$
We also apply bias-correction for the EWMA:
$$ \begin{align} V_{dW^{[l]}}^{corrected} = \frac{V_{dW^{[l]}}}{1 - \beta_1^t} \\ S_{dW^{[l]}}^{corrected} = \frac{S_{dW^{[l]}}}{1 - \beta_2^t} \\ \end{align} $$
Finally, the weight update looks like:
$$ \begin{equation} W^{[l]} = W^{[l]} - \alpha\frac{V_{dW^{[l]}}^{corrected}}{\sqrt{S_{dW^{[l]}}^{corrected}}+\epsilon} \end{equation} $$
In a nutshell, Adam combines momentum and RMSProp: it adds inertia towards the minima, and it also dampens out the oscillations by using the second moment (squares) of the gradient.
An important thing to notice is that since Adam combines momentum and RMSProp, we need two hyperparameters now: $\beta_1, \beta_2$. In practice most people don’t search over these hyperparameters and use default values:
- $\beta_1 = 0.9$
- $\beta_2 = 0.999$
- $\epsilon = 10^{-8}$
Learning Rate Decay
You might hear that RMSProp or Adam have adaptive learning rates. However, we should think of these as two separate things. On the descriptions above, the learning rate $\alpha$ never changes. However, we can combine the approaches described above with learning rate decay for better performance.
Learning rate decay is a pretty simple idea: as we get closer to the minima, we want to take smaller steps in gradient descent; that is, start with some $alpha$ and keep reducing that by some amount every time to we make a step. The reason why we want to do this is that we might be running circles around the minima if the cost function has a degenerate minimum, and therefore take longer to converge.
There are many ways to do this, but the one described on the course is that we will decrease $\alpha$, the learning rate, by some fixed amount every epoch of training:
$$ \begin{equation} \alpha^* = \frac{1}{1 + \text{decay\_rate} \times \text{epoch}} \alpha \end{equation} $$
Notice that $\text{decay\_rate}$ is another hyperparameter to tune via hyperparameter tuning.
There are other learning rate decay approaches, such as exponential decay, that work well in certain settings.
Andrew mentions that tuning the learning rate decay should be pretty low in the list of priorities. Getting a good value of $\alpha$ is much more important.
The topic of non-convex optimization is huge, wide-ranging and beautiful. A lot of the ideas presented in the course are part of ongoing research in the field. The course does a great job at describing modern approaches superficially, but there’s many rabbit holes to go down in. To motivate this, checkout this pretty animation of how different optimizers navigate a complicated cost function:
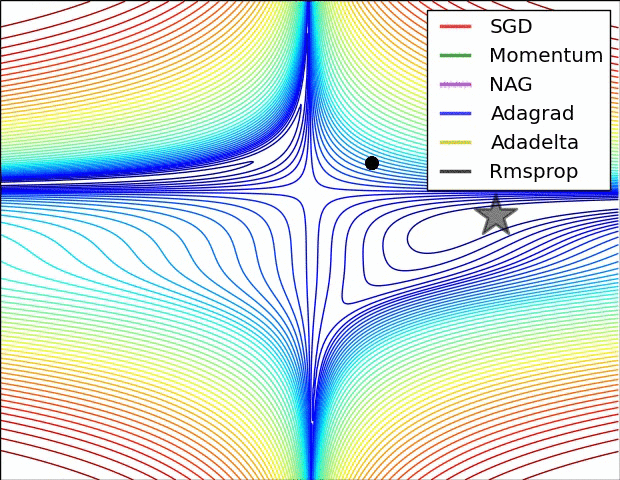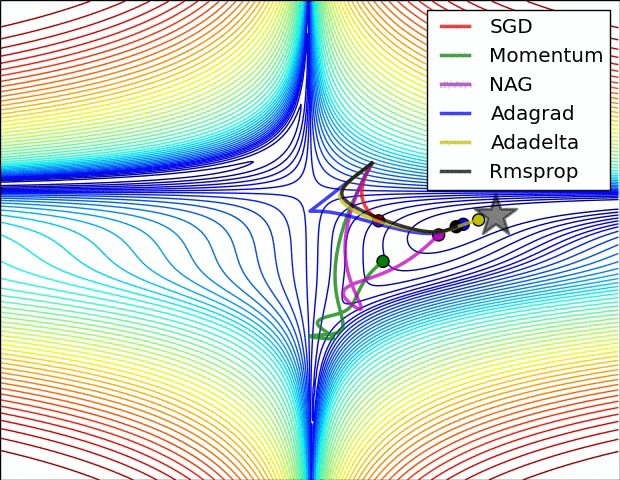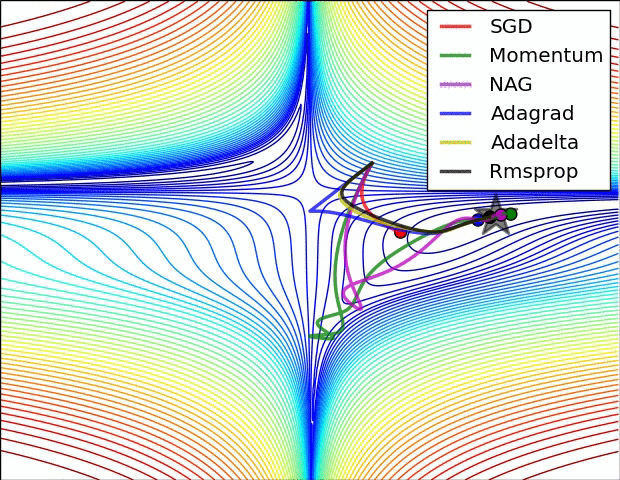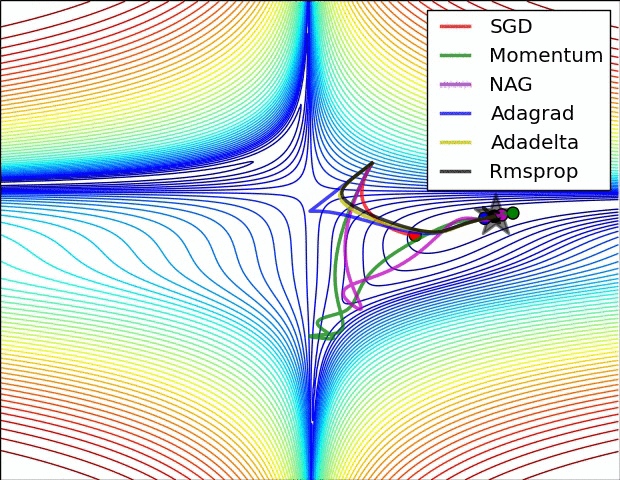
Visualizing Optimization algorithm comparing convergence with similar algorithm
Also, in the case of a long valley:
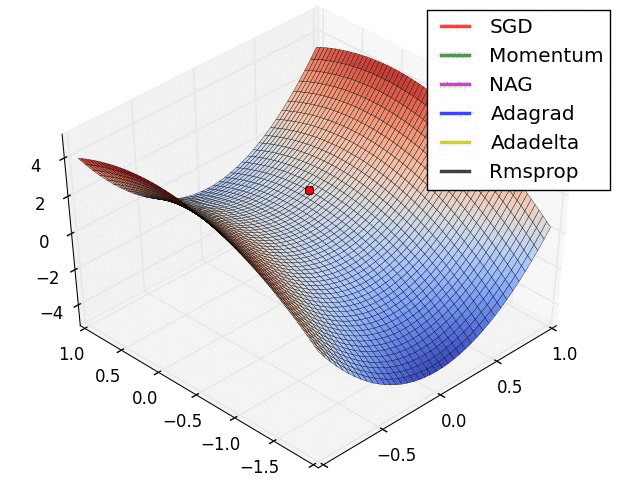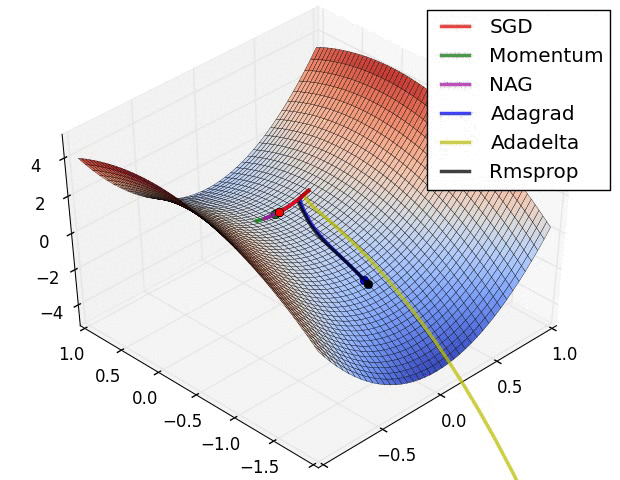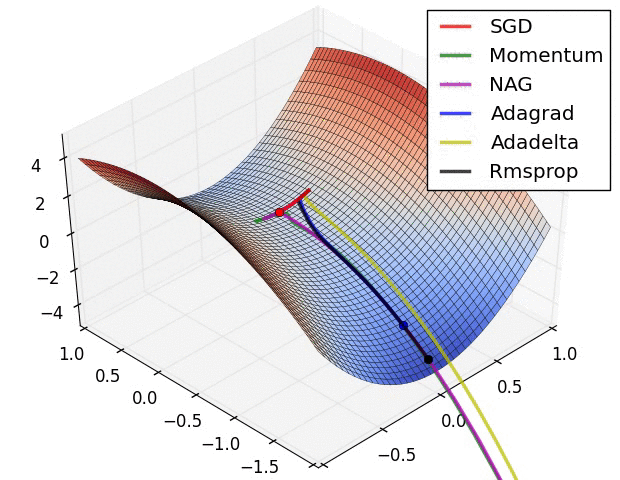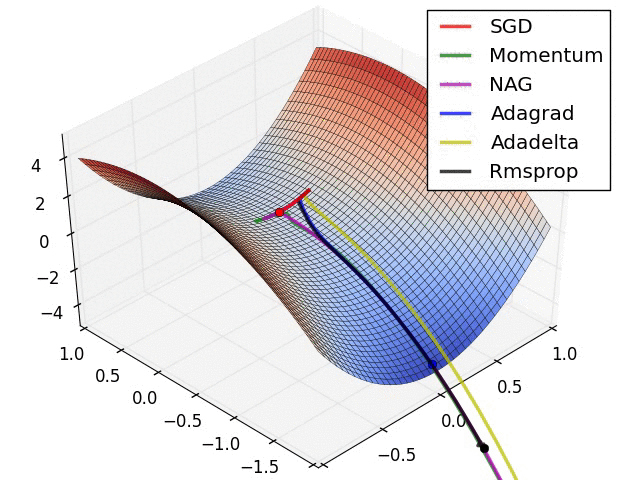
Visualizing Optimization algorithm comparing convergence with similar algorithm
Next week’s post is here.